STRUCTURED PROCESS IN SCIENTIFIC EXPERIMENT
K. W. Pledge
"In this work more than any other it is rewarding to keep on looking at questions, which one considers solved, from another quarter, as if they were unsolved." Wittgenstein
Systematics Vol 3 No 4 1966
ABSTRACT
In this paper the
consequences of applying a certain type of symbolic method of investigation are demonstrated by its
application to the study of
particular scientific experiments. It is demonstrated that the scientific situations
which are called experiments are bound by the same qualitative laws, structural principles, modes of
patterning—however they may he called—as
any other situations in which the presence of completing processes
can be discerned. There enter into scientific work, as into every activity of whatever kind, certain qualitative and
structural considerations which have
direct bearing upon what can be realized by means of action within
situations. Using Gurdjieff's generalized action symbol of the enneagram, which symbolizes the various
patternings to which completing
processes conform, it is demonstrated that both
PREFACE
I. STUDY AND
EXEMPLIFICATION OF STRUCTURE
II. PATTERN OF STRUCTURING
SYMBOLIZED BY THE ENNEAGRAM
III. APPLICATION OF THE SYMBOL TO
PARTICULAR SITUATIONS
IV.
1. Situation
2.
3. Structure of
the event
4. Inner
Harmony
V. OPTICAL
PRISM SPECTROMETER
1. Measurement
Space
2. Structured
Process
3. Setting
up Procedure
4. Three fold
Structure
TRANSFORMATION
CONCLUDING REMARKS
PREFACE
In
this paper an attempt is made to show how certain extremely general ideas about structure are actually exemplified
in the real situations of specific physical experiments.
I do not expect to have achieved more than an indication of how this can be done. It is now little more than two years since I first
began to be able to see how precisely the octave
structure of a completing process, with its necessary interventions
from outside the process, is exemplified in
the simple experiment of Isaac Newton to disperse white light through a prism.
What I
first saw was communicated in a very brief internal paper delivered to the Integral Science Research Group of
the Institute in 1963,* but the time
was not yet ripe to develop the ideas it contained and I left the matter there. For a long time I
ceased even to be able to see what I saw then, for my attention came to be
occupied with other matters.
* I.S.E.R.G. The Group has now
itself been dispersed, owing to the relentless pressure
of the current education research programme of the Institute.
When
I recently took up the task of making a full-length article out of that early paper I discovered that my power to see structure had moved
on even in that short while. I could now see more in the simple physical situation of
I
must apologize in advance for the unfair demand which is made upon the reader who is not already familiar with
Gurdjieff's extraordinary hook All and
Everything or Ouspensky's faithful record, in his book In Search of the
Miraculous, of Gurdjieff's early teaching about general structures and the principles according to which they are held together.
It was Ouspensky's book which first gave me a
convincing glimpse of the way to see into the general structure
of situations. But my rigorous scientific training
was equally compelling with its evidence that science can and does
discover, but in a different way, valid knowledge about the way the world really is.
It was for me a
most happy moment when I saw that both my painfully-acquired empirical science and
the no less painfully-acquired structural ideas of Gurdjieff—which he
himself gained by direct contact with
ancient traditional sources—could be seen to have their own place. The one illuminated and completed the other. I
began to see that Gurdjieff’s ideas
and symbolism could begin to explain why the practice of science can be beautifully exciting and
rewarding for theorist and experimentalist
alike.
I saw that my training as a scientist, which refused to let me accept ideas without seeing for myself sonic kind of correspondence between them and what for me was the unshakable concrete reality of experimental
fact, had not been wasted.
I knew I was seeing new things and looking at old things in new ways that made them meaningful and worthwhile and that was enough.
It became clear to me that the very notion of proof in general
turns upon the possibility of establishing
correspondences between corresponding elements in a
structure. Where no correspondence can be established there is no possibility of proving anything whatsoever. The ability to "follow" a proof therefore becomes the
power to perceive the correspondences involved.
The ability to follow general proofs of the exemplification of general
structural principles turns then upon a power of
the mind to perceive in what we may call a symbolic or figurative
way.
/. STUDY AND EXEMPLIFICATION
OF STRUCTURE
Symbolism refers to pervasive structure. Situations may be more or less structured, more or less intelligible. It is
common experience that structural
features of one situation can often be transferred to another. The use of electrical analogues in treating
acoustical problems is but one example. There are mathematical formulae such as
the wave equation, mathematical
techniques such as the differential and integral calculus, the very operations of arithmetic and number
generally, which provide symbolisms
and refer to pervasive structure in countless situations. In this paper we shall be concerned with the application
of a special kind of structural
symbolism which is non-mathematical but pervasive nevertheless. It is a symbolism specifically concerned to
elucidate the action structure
of situations. In
this paper, specifically those concerned in scientific
experimentation.
Science
is what scientists do. In studying what scientists do we have to study structured action-situations which involve arrangements and operations with extended material objects.
We have to examine closely the adjustments that scientists make when they
set up and operate their apparatus. We have to study the processes which the
apparatus is specifically set up to study.
We have to have some means of eliciting the significance of all these things and we have to find a means of doing
it simply, clearly and with
satisfying generality.
Experiments give data which arc factual. But the performance of any
actual experiment involves considerations of intention, value, judgment, intelligent action towards the achievement
of purposes and the like, which go
beyond the kind of facts yielded by the experiment. They are involved in arriving at the facts, but by the
time the facts have been produced they have disappeared. I his leads to certain
naive misunderstandings concerning the nature of scientific facts
in which the experimentalist himself,
who knows just how much time, effort and difficulty are involved in producing the results, is not
likely to share. Nevertheless, many
men still talk as if the results of experiment are somehow objectively true and independent of the scientist who provided
them. There is some truth in this
notion, but like many another popular belief it requires to be taken with a grain of salt and hedged about
with provisos before it becomes of
real significance.
Generalized symbols cannot be
used without importing into the situation just those
kinds of considerations which are left out in deriving the results of science. Because of this, the manner of their use is
somewhat different from, say, mathematics in scientific work. With them, one
studies whole structures. If a part is studied using such a symbol,
it is by reference to the whole situation from which it derives and to
which it refers. In mathematics it is
possible, and indeed necessary, to study parts in isolation and treat
them as if they are independent from the wholes to which they refer. In generalized symbolism this is not
possible. The connectedness is
primary.
The use of such symbols as instruments of study requires a type of perception of the structural similarity common to diverse situations which is not markedly different from the kind of perception by which
one, for example, learns through study and practice eventually to see what type of mathematical form corresponds to a definite physical situation. The difference is that one is working more from the general form to the situation than seeking to fit one of a
variety of forms to the particular physical
conditions. There is in both cases an aesthetic faculty involved in the
recognition of the correspondence involved which is akin to the response to a work of art.
The
difference from working with mathematical forms lies in the way in which the perception penetrates into the investigation. When one
has discovered the appropriate mathematics for dealing with a particular physical
problem, there often remains only to apply its associated procedure of calculation and the problem is solved. In
other words, the solution can be
arrived at automatically without more ado. In studying the structure with the use of generalized symbolism
the attention cannot leave the
problem lest the substance of the structure vanish before one's eyes. The
practical use of the symbol is rewarding only when it proceeds hand in hand with deliberate confrontation of
the symbolic structure and the "irreducible
and stubborn facts" of the situation under study.
Gurdjieff himself
put this in a nutshell by his reported remark: "Only what a man is able to put into the enneagram does he actually
know, that is, understand. What he
cannot put into the enneagram he does not
understand."*
* Quoted by his pupil, P. D. Ouspensky in In Search of the Miraculous, Routledge & Kegan Paul, 1950, p. 294
The emphasis is on thorough grasp of the situation. In this there is no
difference in degree between the college professor and the skilled garage
mechanic. The practical test is, as always, that of effective action.
Human
situations only comparatively rarely exemplify the full structuring
of a completely general symbol. In particular, most artificial situations fall short of full exemplification,
though elements of it may be perceptible. What one usually finds is that
a situation contains features which
correspond closely to one or another characteristic of the structuring
a symbol describes and lacks others to an equally noticeable degree. Very many situations are found which exemplify the
structure of a completing process.
Others, rather more rarely, clearly show the pattern of three interacting processes necessary for the
attainment of some desired end. Even more rarely do we find that inner
recurrent pattern strongly established by
which they are marked out as realized events.
II. PATTERN OF STRUCTURING
SYMBOLIZED BY THE ENNEAGRAM
We shall in this paper use the action symbol called the enneagram as an instrument of study and interpretation. It will be convenient at
this stage to recapitulate some of the more striking
characteristics of the structuring
characterized in the enneagram before attempting to demonstrate how the whole patterning is exemplified in the
examples that follow:
The symbol can
first be looked upon as the symbol of a completing process of development. This is symbolized by the circle which contains
the "figure of nine lines" from which the name of the symbol is
derived. The process is to be
imagined as originating from the uppermost point and developing along the circumference generated by
clockwise rotation about the centre
point.
The completion of
the development is symbolized by the termination of the curve in its meeting with the starting-point and so forming a completed closed figure. Thus the bounding circle
symbolizes the notion of a continually modified developing process in some
way under restraint by an intentional act of
will which enables it to come to its completion.
The end of the
circle returns into the beginning; and this symbolizes the manner in which a co-ordinated sequence of actions sets out with the end already in view, already present though
not yet in existence.
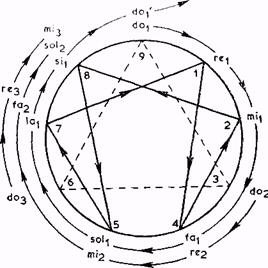
Fig. 1 The
Generalized Action Symbol of the Enneagram showing its Three Interacting Processes
The
circle once completed has no beginning and no end. This symbolizes the power of completed processes to perpetuate themselves repeatedly. Once made
they alter the course of things. As an historical experiment, once made, cannot be unmade but must
be taken into account in future
science. The recurrence of the circle also symbolizes that processes can grow and develop in force and
significance. As the simple process of
The
enclosing circle also symbolizes the requirement for isolation of a region within which the completing process may proceed. In order for an
event to come about there must be some place at which it can be
situated. An event is a really existing situation within the existing
world which has "found its place" and holds on to it with a force of
its own independent of the extraneous
background of ever-changing contingencies.
Here we begin to touch the kernel of the matter and find a connection with science. Science is concerned with the
study of order within the existing world. It
carries on this study by producing and examining artificial situations
from which contingency is, as far as is humanly possible, removed. These situations are called experiments and
are the source of restricted but non-contingent information about completing
processes within the world.
The setting-up of an experiment is the establishment of an event within a completing process. The power to remove contingencies is the condition of establishment of such events. More exactly, it is not the power
to remove but to circumvent contingency
which is the hallmark of the great
experimentalist. Aston, Faraday, Michelson,
* Cf. Brighter Than a Thousand Suns, by R. Jungk,
Penguin Books, I960, and /. /. Thomson and
the Cavcndish Laboratory, by Sir G. P. Thomson,
Nelson, 1964; Reason and Chance in
Scientific Discovery, by R. Taton, Sceince Editions, New York, 1962; The Art of Scientific Investigation, by W. I. B. Beveridge, Heinemann, 1950.
The difficulty
with the application of generalized action symbolism which does not arise with mathematics is the multiplicity of meaning.
Whereas in the more familiar symbolisms there is a more or less one-to-one
correspondence between symbol and meaning, in structural action symbolism the
correspondences are one-to-many and correspondingly complex. Thus the inner triangle of the figure
symbolizes the requirement that
not one but three independently derived and mutually interacting processes of development are necessary to
ensure that one single such process shall be enabled to reach completion.
The
triangle also serves to symbolize that the three processes must knit
together according to the relationship of affirmation, denial and reconciliation specified by the three-term system
or triad. The first completing
process transmits the affirmation in the relationship as the main process
of the three. The second transmits the denying impulses to which the first is subject in consequence of hazard and
uncertainty and contributed perforce by the environmental conditions
through which it is required to proceed. The third process is concerned
with bringing the development successfully to its intended conclusion through a
reconciliation of these two
oppositely-acting impulses.
Another aspect which the triangle symbolizes concerns the qualitative and quantitative aspect of the interaction between the processes. The three impulses must be matched—must be of the appropriate
kind and degree for correct matching and
consequent fineness of quality in the final product.
A striking example occurs in the spectrometer where the inner triad of collimator, prism and telescope allows of astonishingly fine matching in the whole process and an accuracy of
measurement to fractions of a per cent in use.
The triple demarcation of the circle brought about by the inner triangle serves to indicate three main regions of the developing
process. The first region is concerned with a stage of outgoing
or expansion, the second with interaction or
mediation, the third with return or concentrative receptivity. The third region concerns the finalizing process
which intervenes at point 6 of
the figure and ensures proper completion of the process at point 9. The second region is concerned with enabling the
main process to continue and involves the entry of the second process at point 3. The first region is the domain within
which the original process becomes
established.
There are countless further interpretations of the inner triangle of which we may mention only one. This is connected with the location or fixation of a structure within a situation. There is a threefold
action which, once accomplished, ensures that the
parts of a process are harmoniously disposed with respect to it.
In scientific work this is directly concerned
with the location of apparatus in space. There are three kinds of spatial operations possible with apparatus: it can
be placed in position, its elements
can be aligned with respect to directions defined amongst themselves, and finally there can be rotations of directions
thus defined, These three possibilities
exhaust the instrumental possibilities allowed by space.
We can
now come to consider the recurrent figure within the circle. This repeats itself according to the recurring number
sequence 142857 . . . .* The pattern signifies an interwoven connectedness between
the structure of the three processes of the situation which, when attained, organizes the whole into a significant event. Correspondences
are necessary between the points in
the three processes connected by this figure which are made to hold by certain
actions performed between them. The performance of these actions is the work of synchronization between
the process which makes a patterned
and properly working whole.
* The repeated decimal common to all non-integral fractions with 7 as
denominator. It demonstrates the
incommensurability of sevenfoldness with unity and serves
to express in number symbolism one of the necessary incompatibilities of structure. A derivation of the figure is contained in In Search of the Miraculous, p. 289
We come now to the symbolic notation of the musical octave with its seven intervals between the eight notes from do to its
first harmonic do'.
do — re —
mi / fa — sol —
la — si / do'
The gaps marked
with oblique strokes indicate the two semitone-intervals in the octave.
This is an ancient means of
indicating the characteristics of a developing
process in a convenient and economical way. The transition from
note to note successfully conveys the character of a transformation. The
note remains a note, that is, it remains a sound, but changes in pitch. Thus, by analogy, a transformation involves a
change in quality of some material
vehicle which retains its own nature during the change. The transition to a finer quality is conveyed by the
rise in pitch involved.
The
semitones between the notes mi-fa and si-do' symbolize two kinds of discontinuity implicit in the development of completing
processes by which they require to be
reinforced by the intervention of other processes
in order to reach completion. This has already been treated above by reference to the enneagram and the three interacting processes it requires.
There is a special
condition in the transformation process associated with the transition following the note sol which is described by
Gurdjieff .* This lies between the
two steps of the transformation involving the semitones referred to above, at a stage of the process
where interaction with disturbing
factors has already occurred. That point is just being leached at which correcting effects which will
bring the process to finality are at
last able to intervene. It is, in other words, a stage of particular hazard
for the completion of the process to which it refers.
*Cf. All and Everything by G. Gurdjieff, Routledge & Kegan Paul, 1950, p.
754-5. "Harnel-Aoot"
Generally
speaking, it is sometimes possible, in highly sophisticated and well-organized situations, to trace
strong exemplification of all the component structuring of the enneagram pattern.
Such situations are invariably those
which have evolved painfully over the years to meet more and more completely and appropriately some
fairly well-defined need or purpose. They arise in science in those experimental
arrangements which have become evolved
to deal experimentally with one particular phenomenon in one particularly specialized way. A striking example will be studied in the present paper when we come
to examine the structure involved in
the operation of an optical spectrometer and elicit its exemplification of the enneagram
structure. Nevertheless, the enneagram
can be to some extent studied piecemeal by picking out, say, the three-process structure of a petrol-engine where
the main completing process concerns the air, the secondary deals with
fuel injection, and the third ignition.
Another example occurs in the thermionic diode with a strongly
exemplified main completing process from cathode to anode.
We
have now barely outlined the weapons of attack upon the structural problems with which we are concerned. As
described above the striking power of a generalized
symbol is probably only dimly evident. It will become clearer only when we have succeeded in demonstrating a real
correspondence between the patterns it manifests and the structure of the concrete world of scientific experiment.
III APPLICATION OF THE SYMBOL
TO PARTICULAR SITUATIONS
It
will be convenient to approach the study of situations which exemplify the pattern of structure depicted by the enneagram in a
certain order. We adopt the following
procedure:
1
First we shall seek
for the isolated region within which the process proceeds. Strictly speaking, the three do's of the three processes are generated from outside this region. This serves to define its
boundaries.
2
Next we shall
consider the fundamental completing process. Often
we can recognize the similarity between the two notes do and do' which initiate and terminate the process.
3 We shall then look
for the manifestation of the inner recurrent figure of the symbol. Very often
it is this only which gives the clue to the real
character of the event which is realized upon its closure.
4. Finally we shall examine
the situation according to the various meanings of the inner triangle symbol: the three interacting processes;
the fixation of the whole within its situation; the qualitative and
quantitative aspects of the relationship; the three regions, etc.
We now continue,
without more ado, to conduct our studies through the consideration of particular physical experiments. The experiments chosen are
IV
I
Situation
"I do not know what I may
appear to the world, but to myself I seem lo have been only
like a boy playing on the seashore, and diverting myself in now and then
finding a smoother pebble or a prettier shell than
ordinary, whilst the great ocean of truth lay all undiscovered before me."
This
same man wrote the awe-inspiring Principia and the famous Optics.
When we turn in the Optics to the pages at which Newton records his own description of the experiment by which he
demonstrated the formation of the
coloured spectrum from white light, we read the following: *
"In a very dark chamber, at
a round hole, about one-third part of an inch broad,
made in the shut of a window, I placed a glass prism, whereby
the beam of the Sun's light, which came in at that hole, might be refracted upwards towards the opposite wall of the chamber, and there form a coloured image of the Sun."
* Optics, by Sir Isaac Newton.
We now apply the symbolism according to the procedure outlined above.
The
circle, taken as providing the place within which the completing process and potential event is to become
established is, of course, the "very
dark chamber". It is dark because the event is to be an experiment with light, so it is specially prepared. It is a
chamber which will contain the experiment.
2.
The seven steps and eight notes of the main completing
process with reference to which the experiment is made are quite well enough
described for the purposes of exposition. We
can recognize the following eight necessary stages of the process from his
descriptions:
do1 The
Sun as light source
re1 The
hole
mi1 The
entering beam
fa1 The refraction
sol1 The
prism
la1 The
upwards deviation of the refracted beam
si1 The
opposite wall
do’1 The
Sun as coloured image
Table 1. Main Completing Process of
The correspondence between the Sun as
original radiating source •Hid the image as re-radiating source
unmistakably points them out as do and do' of the main completing process. The interval between the
notes mi-fa is
filled by the prism face and so the second process in the experiment must be concerned with the effects of the prism upon the light. The remaining si-do' semitone
interval is filled and the process completed by
the atoms of the wall surface as it absorbs and re-emits the deviated beam incident upon it.
It
is clear that seven steps can be roughly distinguished in this way but, unlike other ways of approaching problems, we have to face an unavoidable seeming vagueness in attempting to make
precise ascriptions. The generalized symbolic method studies situations as
connected wholes; and this holds good throughout.
We cannot make precise and separate from one
another elements which are in reality always connected. All we can
do is point to certain nodal regions within which a given character is more or less exemplified and then pass on to
the next such nodal region by a kind
of withdrawal of the attention from one character and transfer to the next. The technique is exactly in
correspondence with the procedure by which we ascribe seven colours to the
spectrum. We cannot say where one colour terminates and the next
succeeds, nevertheless we can distinguish
the seven—no more and no less.
3. Structure
of the Event
We have enough material now to begin to construct the enneagram of the experiment. To make the whole study more clear, we first put down a schematic diagram of
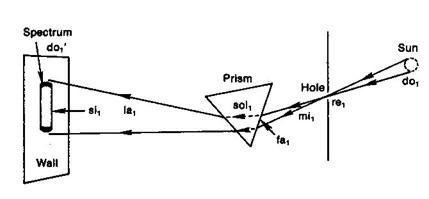
Fig. 2 Schematic of
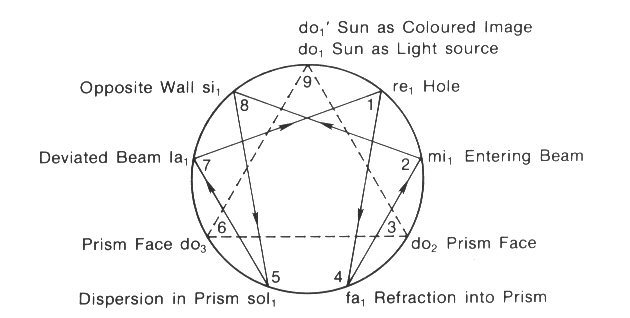
Fig. 3 Enneagram Indicating Octave of
Main Completing Process in
The inner triangle is dotted-in for completeness, but for the moment we shall concentrate on elucidating the significance
of the inner recurrent figure joining the
numbers 142857 ... on the circumference of the circle.
For
this purpose we simply have to turn again to
(1 -4) Connection
From
the first quotation above we extract the following
statement .which describes his first action
in setting-up the experiment. It corresponds
to the establishment of the line 14 of the recurrent figure. It is simply that: ". . . at a round hole ... I placed a glass prism. . .." This is an action which places hole and
prism in a certain state of connectedness
and meaning for each other. The action is simply performed but its significance takes some little time
to comprehend. It sets the stage, as
it were, for the synchronizing actions which will follow in the inner recurrent pattern.
(4-2) Connection
The next
sentence immediately succeeds that previously quoted: "The axis of the prism (that is, the line passing through the middle
of the prism from one end of it to the other and
parallel to the edge of the refracting
angle) was in this and the following experiments perpendicular to the incident rays."
This selling of the prism axis perpendicular to the incident beam is of immense significance. It is an act of standardization which
immediately eradicates one of the contingencies in
the situation, an act of limitation which removes certain
possibilities and retains only a single ordered set. For each one of the set of possibilities which is retained there is one and only one condition of connectedness
holding between prism face and incident beam.
(2-8) Connection
This connection is only weakly exemplified in this experiment, as will become clear when we discover it strongly made in
the spectrometer. At present we need merely note
that a connection between beam and opposite wall
is assured by the construction of the room. The incident beam will always
provide some result at the wall as long as the actions so far described which connect the points 142 are not revoked.
(8-5-7) Connection
For elucidation of these connecting acts we again appeal to
Turning to the
enneagram figure, we plot the action as follows: With his attention directed to the wall at point 8,
(7-1) Connection
Now we come to the act which makes the whole experiment into an event.
To see the connectedness here in its
dependence upon deviated beam and hole, we have to
reflect that the perfection with which this last act is completed depends in the last instance upon the precision with which the point of minimum deviation is able to be determined. This is set directly
by the hole—too small a hole will provide too dim a final image, leaving out of account diffraction effects—too
large a hole will just give a blur.
Hence the adjustable slit of the modern spectrometer. The problem only becomes properly resolved when monochromatic
beams are used, which correspond to
modification in do-i and hence fall outside
the domain of the experiment as such.
4,
Inner Harmony
The wealth of symbolic meaning in the inner triangle of the figure precludes any attempt to give other than a few examples of its
application to the experiment. We shall
consider its establishment by degrees, as follows.
Point 9 is established even before the
prism is placed in position and even before the
experiment exists as the one we are studying. It is established when the initiating and completing notes sound as one. In
other .words, when the Sun simply casts its own image
upon the wall opposite the hole in the
window. There is no triangle because there is no interaction, no outgoing and no returning.
Points 3 and 6 are established, and
with them the base of the triangle and its two
sides 93 and 69, when the prism is interposed between hole and
wall.
With the prism placed in position there comes at once a threefold
separation of the form described above. A completing process comes into being
which comprises regions of outgoing and returning mediated by interaction.
In considering the further significance of the triangle we may visualize
it as a skew,
or asymmetrical triangle so long as the outgoing and returning processes
are lacking in mutual adjustment. When they become balanced (here enters a harmony
into the whole situation. In
The very
experiment itself becomes symbolic of harmony at this point. The structure of harmony cuts through all levels and shows
itself in all acts of harmony
wherever and whenever they may be performed.
The act of harmony signifies a realization of value within a factual situation. Anyone who has actually performed this very experiment will instantly recall the aesthetic satisfaction of
achieving the minimum deviation position at the
end of the setting-up sequence. There is an unmistakable awareness that something has been realized which
comes with the final adjustment. It. is the reward of the true
experimentalist.
V. OPTICAL PRISM SPECTROMETER
We now part
company with the writings of
We pursue our chosen line of attack by first considering the spectrometer in its capacity as the place of experiment.
At this point we are compelled by reason of limited space to refer the
reader to the usual textbooks and laboratory manuals for details of the appearance, construction and operation of the
instrument.* In this paper we shall
assume the reader to be familiar enough with its working to be able to follow the points we shall select
to illustrate our purposes. A
schematic diagram of the optics involved in the instrument is given below.
*
Textbook of Light, by G. R. Noakes, Maemillan, 1946, contains much of the relevant information. Another valuable source is Experimental Optics,
by Wagner, John Wiley, 1929, but any textbook of
Physics to Intermediate Standard is suitable.
In
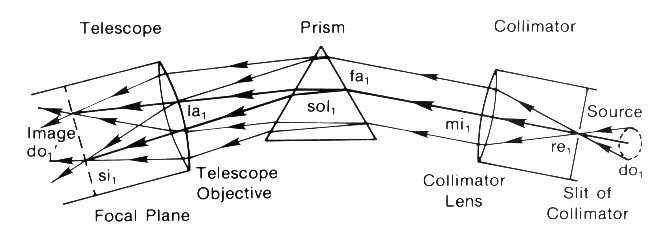
Fig 4 Schematic of Optical
Prism Spectrometer
1. Measurement
Space
The spectrometer as the place within which the experiment will be situated
shows an unmistakable evolution from
** Cf. In.Search of the Miraculous. loc. sit. p. 288
Both of these sub-instruments are within the place at which the same experiment
as before will become situated within the existing world. But the place itself has moved on from
The step forward consists in the previous setting-up, at the
place where the experiment will become situated, of
another space which is so structured that
certain kinds of events taking place within it will inevitably become measured.
This step marks the completed transformation of the situation of
When
the spectrometer is first taken out of the laboratory cupboard it has to be checked to ensure that the principal axes of the telescope
and collimator move in the same plane perpendicular to the main axis of the instrument, about which both telescope and prism table rotate. When
this condition is attained, the harmony of the spectrometer as a measuring-instrument has become realized.
It can then be used in combination with a gauge* to provide traces
in the measurement space of the displacements in the space which occur when the experiment is performed and the actions
which realize its harmony have all been made.
*
Cf, Towards an Objectively Complete Language, by J. G. Bennett. H. H Bortoft and K W. Pledge, Systematics, Vol. 3, No. 3. Dec. 1965. Sect. IV, Pt 1. p. 220
The whole structured situation is very well symbolized
for our purposes by a schematic diagram of the actual arrangement of the
apparatus elements as a measurement instrument shown below. The central point
represents the central axis of the instrument. The collimator is rigidly
connected perpendicular to it. The first circle represents the prism table which
is free to rotate about the central axis. The second circle represents the freedom of rotation of the telescope about the
same axis. The outer most circle signifies the divided circle which is the scale of
the gauge by reference to which displacements in the measurement
space are traced.
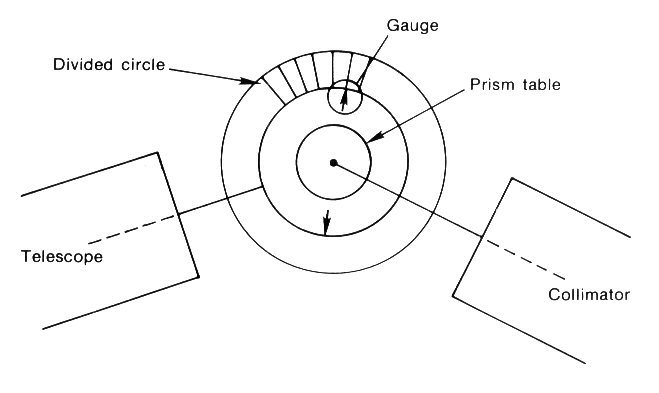
Fig. 5 Schematic of
Measurement Space of Spectrometer
With these observations we leave our consideration of the first aspect of patterning symbolized by the enneagram and exemplified in the
optical prism spectrometer. We have not the space to pursue the study further in this paper, but it should be evident
that the considerations outlined above are of far-reaching importance
for the understanding of measurement as, in general, a contrived technique impressed
upon the structure of the experimental
situation.
2. Structured Process
When we compare the simple schematic of Newton's experiment in Fig. 2 with the corresponding diagram of Fig. 4 for the
spectrometer, we certainly discover refinements
and modifications in the latter; but there can be
no doubt in our minds that the main completing process is in both cases one and
the same.
So we find ourselves in the fortunate position of having two different exemplifications of the same completing process. Hence
we stand a good chance of eliciting, from
consideration of both, their common main octave structure.
We are helped in this by yet another consideration. Generally speaking we find that the effect of all the additional complications of apparatus in the spectrometer is in fact to simplify
the experimental situation. The parallel
beams involved behave effectively in the same way us the "idealized
rays" according to which the refraction phenomenon is usually explained in elementary textbooks. The
corresponding "idealized rays" are drawn in in
heavy lines on the spectrometer schematic of Fig. 4. This supplies us
with yet a third "idealized" exemplification which is particularly clear in showing the features of the
second process.
The Octave Structure
When we consider these three
together we are led to make the following statements
about the notes of their completing processes:
First Process
do1 The sounding of the first note of the main octave consists in the provision of a radiating light source.
re1 The second note concerns the selection out from this radiation of light which is well-defined in direction and solid angle.
mi1 The transmitted light thus defined enters the experimental domain and travels onward by expansion.
Second Process
Interval and do2 A plane surface is interposed in its path. The normal to its surface defining some angle with the beam
now incident upon it. In the
spectrometer a lens at this point ensures that light from the beam is
uniformly incident. The glass surface is the second source in the experiment.
fat and re2
Light in the incident beam enters the prism
surface and interacts selectively there with the glass (hence the
occurrence of re2 here in the enneagram).
sol1 and mi2
The light is dispersed (sol1) and
its path deviated (mi2). These
conditions persist during its transmission through the medium.
Third Process
Interval and do3 The second surface of the prism becomes the exit surface
through which the transmitted beam emerges, eventually to manifest the effects of interactions which it has
undergone. The angle of this face to
the first is a determining factor. The objective lens of the telescope performs certain finalizing functions and, in
particular, gathers together as one
whole emergent beams of corresponding colour and
deviation.
lat, fa2
and re3 In the spectrometer,
the sounding and blending together of these three notes signifies the
finalizing action of "bringing to a focus".
la1 is the condition of the emergent light as carrying
with it the results of all its previous interactions in a form able later to be manifested.
fa2 is "the deviation of the already deviated" at the second prism
face and, in the spectrometer, at the telescope
lens as well. It is another interaction analogous
to fa1 where the incident
beam interacts with the first prism face.
re3 we may take as the definition of directions which
takes place at exeunt from the second prism
face. The directions are directed towards some final or ultimate place at which each and every colour will become
displayed correspondingly.
si1,
sol2 and mi3 These
three notes likewise correspond to the condition of the light "coming to a focus" in the focal plane of
the spectrometer telescope objective lens, or
arriving at the final displaying screen of Newton's
wall.
Si1 is the condition of
the light as being concentrated into seven more-or-less specific definite colours.
sol2 is the fixation and final dispersion of the effect of the prism
refraction by the formation of the whole spectrum in consequence.
mi3 manifests as the persistence within one well-defined spatial region
of the image forming the displayed effect which is the spectrum.
do'1 signifies
the image as being itself a re-radiating light source. As such, it forms the first note of another
consequent octave by which it comes eventually to be perceived. This
second octave is taken for granted in the
whole previous treatment. Nevertheless, it is evident that the experiment begins from do\ just as much as it
does from do’1. The whole is designed to provide material for observation via
the display at point 8.
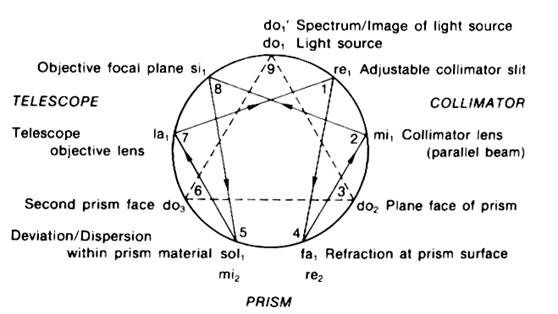
Fig. 6
Enneagram indicating main octave of Spectrometer
The
ascriptions of the notes in the octave here derived are quite precise enough for our present purposes. For the moment we need only note
that the two lenses are placed at points 2 and 7 respectively in Fig. 6. We might have expected them to fill the two
intervals at points 3 and 6, as indeed
they do. But it should be clear from Newton's experiments that these two
intervals are already filled by the two prism faces and that therefore the lenses may quite plausibly play other
roles in the whole,
It is
characteristic of structuring considerations that one and the same clement may play different, though perhaps
closely similar, roles when considered as entering into different
kinds of structure. In much the same way a
piece of paper may in different situations serve as a bookmark, a place
to record a telephone number, or a dollar bill. Which role is appropriate depends upon the total context under
consideration.
3. Setting-Up Procedure
We
continue our study of the action-structure of the spectrometer by examining how the inner recurrent figure is
manifested in its operation. It will be evident from the previous
discussion of the same figure with reference
to
Reference to the
usual textbooks of experimental physics soon discloses that a standard procedure has evolved for this over the years. This
procedure is always followed if one wants to line-up a spectrometer accurately with the greatest economy of action. A
typical textbook of this kind* reads:
"Before proceeding to make measurement with the spectrometer it is necessary to see that certain conditions hold true, as follows:
1. The principal axes
of the telescope and collimator must be perpendicular
to the main axis of the instrument, i.e., the axis about which the telescope and prism table rotate.**
2. The telescope must
be focused for parallel incident rays, that is, for infinity.
3. The collimator
must be focused for parallel emergent rays.
4. The prism must be
adjusted so that the faces which include the angle to be measured are both parallel to the axis about which the telescope and table turn.
Wagner adds the two further
conditions:**
(a)
The axes of telescope and collimator must pass through the main axis of the instrument.
(b) It must be possible to
make the axes of the telescope and collimator
coincident."
* Wagner, loc. cit. p. 24, This book contains the
practical work in optics given to officers at a U.S.
Navy Postgraduate School, some of whom later "will have duty as inspector* of military telescopic instruments to be purchased
for use in
the Navy".
** We note that that this refers
to and establishes the measurement space as described above
in part I of this section.
Wagner then notes that these five conditions "are
to be established in the order given";
and goes on to describe the procedure of doing this in the usual way.
We may begin at
this point to make correspondences with the points and connecting recurrent inner lines of the enneagram, as follows:
Point 8 refers
to the first action in the lining-up sequence, which is the removal of the telescope from the spectrometer and
its adjustment to focus parallel incident rays in the focal plane. This is
usually done by the simple expedient of focusing on any convenient
distant object. This operation connects a certain place—the focal
plane at point 8 with the condition of various
parallel beams entering the instrument: which, we notice, refers to
point 5 where the deviated and dispersed beams are first present in the prism.
Point 2 is the scene of the next
operation. This is the lining-up of the collimator to make it provide parallel beams. The telescope and
collimator literally are "lined-up"
on opposite sides of the prism table while the operation is performed. This establishes the line 2-8 in the figure. The
entering beam for the experiment in any case becomes defined at point 2,
so there can be little doubt of the correctness of our ascription here. Point 4. The
first prism face is then lined-up so as to become parallel to the axis about which telescope and table turn.
This is done by a rather complex set
of adjustment operations which take longer to describe than to do. In
these operations, both telescope and collimator are used in conjunction with the prism face, itself acting as a
reflector. We note that it could not be done if telescope and collimator
were not already aligned. Completion of the
operation really establishes the line 4-2 by which the collimator beam stands
in a well-defined perpendicular relationship to the first prism face.
Point 1 is the collimator slit itself,
which is adjustable. Up until this point in the sequence the experimental operation which produces the phenomenon has been in the background. It now begins to make itself felt
and the collimator slit is made as narrow as is required. In these earlier setting-up operations plenty of light has been an advantage; now
it has served its purpose. In making this
observation we distinguish between the inner
lines 1-4 and 7-1, and find how naturally the sequence moves
along the zig-zag path of 4-1-7.
Point 7. We may regard this point as the point or place in the experiment at which the experimenter enters into or intervenes in the workings
of Nature. It is at tins point that the subtle and delicate operation is
performed by which, it) this experiment, the phenomenon of minimum deviation is actualized. We have already referred to the
beauty of this achievement. It is a
synchronizing operation which, once again, is better and easier
to do than describe. But it very clearly illustrates the action at this point 7
by which all three interacting processes are brought into a single harmony of
synchronous adjustment.
The collimator is fixed in position, thus ensuring the establishment of the first process. The prism and telescope which are the instruments of the other two processes are then used together in one single operation with respect to the image of the slit in the focal plane. This operation
consists in coming to precisely the same condition as did
"Between the descent and
ascent, when the image seemed stationary, I
stopped the prism, and fixed it in that posture, that it should be moved no
more."
We
see this operation as the establishment of the zig-zag line 8-5-7 in this figure.
Point 5 is the place where the material
of the prism and the prism angle determine the dispersion and deviation of
the refracted beam transmitted through it.
In coming to the position of minimum deviation through the operation at point 7, the phenomenon is brought
into a condition at which a
particularly simple relationship holds between the nett
deviation of the coloured beam for
which it is established, the prism angle, and the index of refraction of its material. All these
three have reference to point 5 and determine
the final setting position at minimum deviation. Hence the setting-up sequence terminates at this point.
We ask ourselves why the sequence should begin at point 8 and work backwards along the sequence against the direction of the arrows given
by the recurrent decimal 142857. . . . An answer would seem to be that, unlike
Another
is that from the point 8 the enneagram shows the main completing process
of the experiment as connecting-up to the second enneagram which involves observation via do1. If a
photographic plate is placed in the
focal plane of the telescope the instrument becomes a spectro
graph. When the plate is exposed and
later developed and fixed and the spectrum ii depicts is studied, (he studying
will begin the new enneagram and will
necessarily involve (he experimenter in a much more cognitive role. So, however
the experiment carries on from point 8, it has to be tailored to fit this final
end of producing the displayed spectrum. Hence the various steps of
adjustment begin from point 8 and work back around the zig-zag figure.
At this point we leave the setting-up sequence and carry on to the next and final section of this part of our study. It will be evident
that the attempt to demonstrate the role of the
recurrent figure in the experiment could be carried to almost any depth of
detail and precision. The beauty of the general symbolic method comes largely
from its use as an instrument for studying
situations in depth. There is no end-point at which we can terminate our enquiries with the assurance that there is no more to be discovered. There is always more to be seen, always more to be grasped and understood. The only limit is set by our own will to seek for what is there to be found.
4. Three-Fold Structure
We come finally to
study the spectrometer in some of its three-fold aspects. Since the spectrometer is designed as a three-fold instrument this is an almost inexhaustible task. Since, in
addition, the inner triangle of the
enneagram has an unlimited wealth of meaning, we shall again be compelled to select from the variety of
exemplifications available a few of particular interest for our present study.
Collimator-Prism-Telescope
The
triad set up by the three sub-instruments of the spectrometer is an obvious first choice. Very much can be learned from it of the workings of the triad, the structure of relatedness. It will already
have become apparent that whole experiment is symbolic of the structure of relatedness, down even to very triangular shape of the
prism which makes the experiment what it is, and
was for
The triad of collimator-prism-telescope is not established all at once at the beginning of the experiment. It becomes
established only when the position of minimum deviation has become
achieved—exactly as in
Referring to the
enneagram, point 9 sounds its two notes do1 and do’1
in the spectrometer when the collimator
and telescope have been given such a perfection of adjustment within the measurement
space that they are exactly matched. This occurs for the two
sub-instruments in two roles.
1 As extended material objects playing roles in the triad of the measurement-space, they have previously to be lined-up in such a way that: “It must be possible to make
the axes of the telescope and collimator coincident."*
* Wagner,
loc. cit p. 25. Spectrometer adjustments.
In this condition they coincide as potential angular measurement-objects and express the do, and do\ of the measurement
enneagram.
2. The initiating and completing notes of the experiment sound as one when the image of the radiating light source formed with
light transmitted through the collimator slit is
brought into focus in the focal plane of
the telescope.
Once established, this is a condition which recurs throughout the
experiment in all the setting-up operations. It
is fixed once and for all, as far as the
experiment is concerned, only when that inner harmony becomes realized
by which the recurrent figure is synchronized into one whole and the triad is established.
Three Impulses**
When the prism is
placed upon the prism table the third role in the relationship enters the scene in embodied form and we are able to speak of the three relational impulses which the three
elements transmit:
1. The collimator transmits the
affirmation of the existence of the source of the
first process in the experiment. The fiat lux.
2. The prism transmits a denial
through setting-up conditions by which the
transmission of the light from the first process becomes opposed, limited and subject to fragmentation.
3. The telescope, when used as a
third instrument in relationship with the other two,
becomes able to transmit the means of reconciling
them which is, in the last analysis, the free and independent
reconciling will of the scientist as experimenter—by virtue of which he can perform intentional actions
involving progressive approximation.
**
For further elucidation of the three impulses and the manner by which they enter into different modes of combination the reader is referred to The
Dramatic Universe,
by. J. G. Bennett, Hodder & Stoughton, 1961, Vol. IIPart
II, p. 69 ff. The Triad - Will.
Perfect
Reconciliation
The
prior condition at which the telescope and collimator are perfectly matched corresponds to the condition of their perfect reconciliation—complete receptivity combined with total donation. It is
possible only when the two are not
committed in any way to participation in the interaction
for which the prism acts as a denying source. The moment this denying source enters the situation, the point 9 becomes the
triangle 3-6-9 in the symbol and the perfection of the reconciliation
becomes compromised by denying elements.*
* We note that when the
reconciling source enters fully into the situation there is the completion of
the inner recurrent figure and the triangle 369 becomes the pattern 142857 . . . endlessly recurring. We have not the space to
pursue this observation further here. It signifies the establishment of a
permanent hold upon existence for the event
concerned, through perpetual renewal.
This
corresponds to the establishment of three distinct
kinds of process:
Three Kinds of
Process
1.
The function performed by the collimator so
clearly typifies the outgoing process that it deserves the name of paradigm in
this role.
2.
The prism likewise
typifies the second process which provides the field of interaction, and sets up the condition of denial towards
the first process.
3.
The connection of the
telescope with a finalizing role has been already sufficiently stressed earlier in this paper. It is likewise a paradigm in typifying the returning concentrative process by which a final image is formed.
Power of
Reconciliation
It is a mark of the fineness of quality of reconciliation expressed by the instrument as a whole that it can perform
measurements to an extreme degree of precision. If we look to see how this
quality enters the machine, we see that it all
turns upon the provision and manner of use of the parallel beam.
The
parallel beam presents both collimator and telescope with a common
mediating power, or free energy, which is at their disposal. The collimated beam is an already reconciled entity.
It therefore has the power to engender
harmony into the situations in which it participates. In the spectrometer
this shows itself in the smoother manner in which the light passes through its intervals in completing the
main process of the experiment.
It is helped into the prism. The deviated light is afterwards eased into
position at the final image. There is more harmony in the spectrometer as the place where
VI.
TRANSFORMATION
The process of qualitative transformation by which the steps of the completing
processes transform one into another is triadic. It is expressed by Gurdjieff in a deceptively simple generalized
formula as follows:
"The higher
blends with the lower in order to actualize the middle and thus becomes either higher for the
preceding lower or lower for the
succeeding higher."*
* Cf. All and Everything, p. 751: "A new arising from the previously arisen through the 'Harnel-Miatznel'." The higher stands to the lower in the relation of a greater activity for the situation.
The lower is always more passive than the higher.
We can express the action of transformation by reference
to some of the steps we have already
elicited in the main completing process common to
Entry of Light into
the Experimental Domain
The light radiated out from the presence of the source (doL) blends with the slit and its surrounds (re,)
in order to actualize the beam transmitted through the slit and
thus becomes an expanding cone of light (mi,) well-defined in direction
. . . travelling towards the prism face.
We begin to see
from this formulation just how down-to-earth these expressions and notions of generalized structure are. We are familiar in our everyday lives with the structuring of light
falling upon slits and take it for
granted. In fact, we make many more assumptions about the ubiquity and pervasiveness of generalized
structuring than we usually realize.
We are accustomed to assume as a matter of course that the world is "logical", "coherent"
and "consistent"—and these are assumptions about generalized qualitative structure.
It is noticeable, also, that this kind of
picturing of situations and what is going on in them is
precisely what we come to when we consider the
world as a place for action. In this world we as scientists set up experiments, make adjustments, take readings, produce and
interpret records of results and
diagrams of apparatus. The world of practical science is a world of transformation conceived of in this
kind of way.
We continue with the expression of the transformations involved in the experiment in these terms as follows:
Incidence Upon the Prism
The light present in the
well-defined conical beam (mi1) travels towards and blends with
the presence of the plane surface of the prism
face (do2) in order to actualize a third beam
(fa1) interacting with the glass.
We can also express in this way the effect on the octave of the intervention of the collimator lens into the completing process. Thus:
The intervention of the collimator
lens into the first interval of the main completing
process assists the blending of the incident beam with
the prism face by previously itself blending with it in order to actualize a uniform parallel beam whose
light may . . . etc.
The correspondence
in form between Gurdjieff's generalized formula and the way in which we commonly understand these kinds
of trans-formation is remarkable. It
is clearly a means of expressing the structure of transforming situations whose depth is limited only by our ability to
penetrate into and see what is going on. We can pursue the
processes into the prism. Thus:
Refraction Into the Medium
1. The light present in the incident beam (fat) enters the medium through the prism interface (do2) and blends with the material of the glass
in order to actualize an interaction and thus becomes a
dispersing cone of light (sol1). . . travelling
towards the second prism face within the medium.
2.
The presence of the
plane surface (do2) blends with the material properties of transparency and opacity of the glass (re2) in order to
actualize an interface which shall evenly refract and uniformly deviate into its interior (mi2) the
light paths of beams incident upon it.
Dispersion we ascribe to the light itself and therefore to the condition
denoted by soli.
Deviation being an effect of the prism material we ascribe to mi2. Snell's law, of course,
comes in at this point, when the phenomenon
is related to a measurement space.
Here we may leave the main completing process at a very appropriate
place for the reader to begin to complete the final expressions for himself. Much of the
preliminary ground has already been covered and sufficiently excavated in the second section of this last part.
The exposition given above in this paper of the correspondences which
may be found between the various structurings expressed by the enneagram symbol and features of the structure
exemplified by the experiments
considered may seem somewhat arbitrary and unconvincing on a first reading. The determined and
experimentally-minded reader is invited to consider for himself the
correlations to be discovered between
the symbol and the most economical practical procedure followed in actually performing that
well-known elementary experiment by which
the index of refraction of glass is determined from a sample in the form of a
rectangular block—pins, paper, pencil, ruler, protractor and all. There is a stage in this procedure at which the
experimenter finds it necessary to
move his eye right round from one face of the block to the other in order to
finish plotting the course of the "idealized ray", defined by the lined-up pins, after refraction through
the block. The reader should find,
after only a little difficulty occasioned by the unfamiliarity of the symbolism, that this can he easily and
convincingly correlated with the (2-8)
line in the zig-zag inner pattern. Consideration of the vital role played
by the eye in that experiment, in conjunction with the use of his spatial freedom by the experimenter, is
particularly illuminating. In that experiment,
as with
VI. CONCLUDING REMARKS
I have endeavoured
in this paper to demonstrate empirically the applicability of Gurdjieff's generalized enneagram symbolism to a piece of scientific work. I am sufficiently familiar
with the work in question to be able
to bring both it and the symbol into direct contact. To my mind this is almost certainly the only possible way to
come to some understanding of what this generalized symbol really is
about.
We talk about the power of mathematics, but more generally any symbol
which refers to the structure pervading a real situation has power when used in relation to that situation. The
structure or patterning to which the enneagram symbol refers is so
extremely general that its power as a
device for coming to understand structuring in all kinds of situations must be virtually unlimited. I have no doubt that
this was one of the purposes for
which it was originally created.
The enneagram is a device, in its use a method, for coming to understand
general structural principles. The study of their exemplification in particular situations leads one to a new
view-point which is anti-temporal.
Structure is
timeless and refers to that which remains beyond the actualizations of temporal
process. Processes actualize temporally in accordance with patterns—which
are anti-temporal because they remain preserved
and untouched, unmodified by the changes which take place successively
in time.
The enneagram points to a world which is already present but virtual. A world which is
ordered, structured, patterned - latent with forms of meaning
already waiting to become realized in the actualization of existing situations.
The symbol thus expresses the latent patterning of the present moment*
* Cf. Towards an Objectively Complete Language, by
Bennett, Bortoft and Pledge/ .Systematics.
1, No. 3, 1965.
The
symbol is an obvious representation of the structure of a perfectly co-ordinated process actualizing within a present moment. This
is symbolized by the structural figures
confined within the circle. In an experiment the
central point about which the circle is circumscribed is the will of the scientist S by reference
to whom the whole experiment into existence, is
set up, adjusted, measurements are performed. . . . All that is
compatible with the performance of that particular experiment has its place within the circle; all else is
excluded by the initiating decision of
S. Thus the circle initially symbolizes the compatibility bracket set up
by that act which separates the
relevant from the irrelevant. The setting-up of the inner triad
symbolized by the triangle corresponds to the establishment of a compresence with the basic
apparatus—as the prism establishes the refraction effect by its
compresence with light-source, slit and screen. The state of coalescence comes about when the inner recurrent
pattern is closed. The three kinds of linkages refer to the points at the
corners of the triangle. The three
recurrent elements can be ascribed to the three kinds of processes involved and hence to the three sides of the triangle. The symbol which denotes within-ness has
a two-fold meaning as the connection of circumferential points with the centre
and also the area contained within
the circle. But once again we must beware of trying to tie down meanings which are really many-to-one. The advantage
of the enneagram symbol as compared with other means of representation lies
in its ability to communicate the structural connectednesses
immediately and unambiguously.
I
hope to have shown in this paper that the enneagram symbol is directly relevant to the scientific procedure. But
science is only one of the fields in which human
beings engage themselves with a view to achieving purposes. Wherever
there is something to be done, there is, if it is worth doing, some value to be realized in the doing of it. Satisfaction comes when
the situation within which our efforts are applied transforms from struggle into harmony. When that happens something
has both made and found its proper place within the existing world.